FUNGSI DAN GRAFIK FUNGSI
Assalammualaikum wr.wb. saya muh. Fajar , disini akan menjelaskan tentang fungsi dan grafik fungsi yang memiliki banyak bagiannya, berikut penjelasannya :
Fungsi Kuadrat
Fungsi kuadrat adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Fungsi ini berkaitan dengan persamaan kuadrat. Bentuk umum persamaan kuadrat adalah :
Sedangkan bentuk umum dari fungsi kuadrat adalah:

Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta
Fungsi kuadrat f(x) dapat juga ditulis dalam bentuk y atau :

Dengan x adalah variable bebas dan y adalah variable terikat. Sehingga nilai y tergantung pada nilai x, dan nilai-nilai x tergantung pada area yang ditetapkan. Nilai y diperoleh dengan memasukan nilai-nilai x kedalam fungsi.
Grafik Fungsi Kuadrat
Fungsi kuadrat  dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
 dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
Grafik dapat dibuat dengan memasukan nilai x pada interval tertentu sehingga didapat nilai y. Kemudian pasangan nilai (x, y) tersebut menjadi koordinat dari yang dilewati suatu grafik. Sebagai contoh, grafik dari fungsi :  adalah :
adalah :
 adalah :
adalah :
Pada grafik fungsi ini akan selalu memiliki garis simetris pada x = 0 dan titik puncak y = 0. Sebagai contoh  maka grafiknya adalah :
maka grafiknya adalah :
 maka grafiknya adalah :
maka grafiknya adalah :
2. Grafik fungsi 
yaitu selalu memiliki garis simetris pada x = 0. Namun, titik puncaknya sama dengan nilai c atau
Grafik ini merupakan hasil perubahan bentuk dari  Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut :
Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut :
 Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut :
Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut :






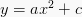























Tidak ada komentar:
Posting Komentar